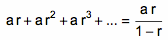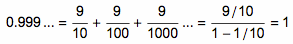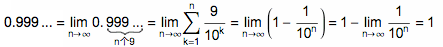leadscloud

Google SEO|外贸营销推广

发表于 更新于 分类于 阅读次数： Valine：

对于一个网站的结构来说，URL的设计也非常的重要，在URL设计时我们应该事先做好规划，应该从用户体验和搜索引擎蜘蛛体验出发，在总体上边应该做到URL清晰、友好、方便记忆，然后还要适当的考虑对于搜索引擎排名的影响，具体来说，URL设计时我们要从下边几点来着手：

1、URL越短越好

这样做主要是为了用户体验，其实对于搜索引擎来说，不超过1000个字母都没有问题，可是如果不考虑用户体验，确实真的用了非常长的URL的话，用户看起来就有些麻烦了，甚至会马上离开你的网站，曾经有人做过这方面的试验，在搜索引擎的搜索结果中，一个较短的URL出现在一个较长的URL下边时，较短的URL的点击率是较长的URL的2.5倍。而且较短的URL也比较有利于复制与传播。人们都比较喜欢简单的东西，特别是现代，人们不喜欢太复杂的东西，能简单就简单。所以网站的URL要尽量的短。

2、URL中避免太多参数

在进行URL设计时，我们尽量使用静态的URL，虽然现代的主流搜索引擎都能够很好的去索引带有参数的动态网页了，可是，使用静态的URL还是有一定的优势的，如果由于某些原因，不能使用静态的URL，而不得不使用动态的URL时，设计的则是URL中的参数应该尽量减少，不要超过三个，一般的情况下URL中的参数2-3个就可以了。参数太多了不但用户看起来困难，对搜索引擎的索引可能也会造成一定的问题。所以，能使用静态就使用静态的URL，能短就尽量短。

3、目录层次尽量少

这里所指的目录层次是指物理目录结构，而不是指逻辑结构，我们在进行URL的设计时，网站的结构要尽量的去减少目录层次，层次不能太深了，一般建议不要超过三层，特别对于一些新站来说，权重低，搜索引擎蜘蛛爬行得很浅，深一点的页面，蜘蛛都很可能不会去爬行的，所以要尽量的做到使目录层次减少，URL缩短。根据观察，百度尤其比较喜欢目录层次比较少的页面。

4、文件名及目录名要具描述性

文件名及目录名要具有可描述性，不但让用户一眼就能看出来这个页面是关于什么的，对用户体验比较友好，而且搜索引擎也比较喜欢这样的URL。例如一个关于新闻的目录，我们可以把它命名为news，用户看到这个目录名称，大概就知道这个目录是关于什么内容的了。

5、URL中包含关键词

关键词出现在URL中，可以提高一定的相关性，尤其对于优化英文网站，这点非常的重要，而且关键词出现在URL的位置越靠前越好，也就是说出现在域名中最好，其次是出现在目录名中，最后才是出现在文件名中。注意一点的是不过不要出现关键词堆积的现象。例如许多朋友的SEO博客，在网站的域名中就包含了SEO，这对于关键词的排名来说，具有一定的权重优势。

6、URL中的字母全部用小写

这里有以下原因：

(1)、全部用小写，用户比较容易输入，不用因为大小写混合而出现错误，这是人们的输入习惯。

(2)、有些服务器是区分大小写的，例如Lunix服务器，这样在站长做链接或者是用户输入时，会因为大小写的问题而出现404错误，而且robots也是区分大小写的，如果大小写搞错了，可能会造成不能收录的严重问题。所以建议所有的URL都使用小写。

7、连词符的使用

目录或者文件名中如果有两个单词组成时，一般建议中间使用中划线(-)隔开，切记不要使用下划线或者其他字符，在搜索引擎中，它是把中划线当作一个空格来处理的，而下划线则是被忽略的，例如seo-lunwen会被读成seo与lunwen。这是比较友好的写法。

8、使用目录形式还是文件形式

大部分的CMS系统都可以把页面的URL设置为目录或者文件形式，有些朋友认为目录形式比文件形式权重要高一点，无论使用哪种形式的URL，权重应该是差不了多少的，基本可以忽略二者之间的权重差异，使用目录形式有一个优点，以后如果更换其他的编程语言，URL也可以不用变化，也不用经过特殊的处理，而文件形式的URL可能文件的扩展名会变化，需要做一定的URL重写处理。

上边是一个网站的URL在设计的时候，应该注意的八个问题。在设计URL时，只有严格的按照这几点来操作就可以了。网站的URL设计得好，不但利于蜘蛛的爬行，而且用户看着也简单、易懂。

 

源地址：http://gowebway.blog.163.com/blog/static/652277201142710172336/

发表于 更新于 分类于 阅读次数： Valine：

内核： Linux ubuntu 2.6.38-8-generic #42-Ubuntu SMP Mon Apr 11 03:31:50 UTC 2011 i686 i686 i386 GNU/Linux

系统版本： Ubuntu 11.04 32位

打开 http://127.0.0.1 显示成功，但打开 http://127.0.0.1/p.php 出现502错误

/root/lnmp restart 错误信息：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
root@ubuntu:~/lnmp0.7-full/php-5.2.17# /root/lnmp restart

=========================================================================

Manager for LNMP V0.7  ,  Written by Licess 

=========================================================================

LNMP is a tool to auto-compile & install Nginx+MySQL+PHP on Linux 

This script is a tool to Manage status of lnmp 

For more information please visit http://www.lnmp.org [local]1[/local]

Usage: /root/lnmp {start|stop|reload|restart|kill|status}

=========================================================================

Stoping LNMP...

Nginx program is stop

PHP-FPM program is not runing!

Shutting down MySQL

. * 

MySQL program is stop

Starting LNMP...

Nginx start successfully!

/root/lnmp: 行 46: /usr/local/php/sbin/php-fpm: 没有那个文件或目录

PHP-FPM start successfully!

Starting MySQL

. * 

MySQL start successfully!

解决办法：

（打开 /root/lnmp0.7-full/ubuntu.sh 找到 echo "========================= php + php extensions install ===================" 按里面的代码执行的。从 tar zxvf php-5.2.17.tar.gz 开始执行的，下面有具体的）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
apt-get install libjpeg62 libjpeg62-dev libjpeg-dev  

ln -s /usr/lib/i386-linux-gnu/libpng* /usr/lib/

ln -s /usr/lib/i386-linux-gnu/libjpeg* /usr/lib/   

cd /root/lnmp0.7-full/ 或者 cd cd /root/lnmp0.7/ 

tar zxvf php-5.2.17.tar.gz

gzip -cd php-5.2.17-fpm-0.5.14.diff.gz | patch -d php-5.2.17 -p1

cd php-5.2.17/

./buildconf --force

./configure --prefix=/usr/local/php --with-config-file-path=/usr/local/php/etc --with-mysql=/usr/local/mysql --with-mysqli=/usr/local/mysql/bin/mysql_config --with-iconv-dir --with-freetype-dir --with-jpeg-dir --with-png-dir --with-zlib --with-libxml-dir=/usr --enable-xml --enable-discard-path --enable-magic-quotes --enable-safe-mode --enable-bcmath --enable-shmop --enable-sysvsem --enable-inline-optimization --with-curl --with-curlwrappers --enable-mbregex --enable-fastcgi --enable-fpm --enable-force-cgi-redirect --enable-mbstring --with-mcrypt --enable-ftp --with-gd --enable-gd-native-ttf --with-openssl --with-mhash --enable-pcntl --enable-sockets --with-xmlrpc --enable-zip --enable-soap --without-pear --with-gettext --with-mime-magic

make ZEND_EXTRA_LIBS='-liconv'

make install

这个问题我在vpse论坛上问过了，上面有关于我如何解决的：

http://bbs.vpser.net/thread-3055-1-1.html

附：

LNMP安装教程
LNMPA安装教程

发表于 更新于 分类于 阅读次数： Valine：

 

由于都是Gif格式文件，所以打开比较慢，请大家耐心等待！
动画图解一般看不见的机械原理——更新多款发动机，手枪——现代生活离不开各种机械，无数复杂的机械走进了我们寻常百姓的生活中，小到我们家里客厅墙上的挂钟，大到出门上班用以代步的汽车，都离不开机械在其中默默的工作。不知道你有没有偶尔想问，究竟是什么样的机械，通过怎样的方式在运转，让我们的生活更便利呢？ 

平日里，我们习惯了在产品外观上品头论足，感慨设计师的精彩创意，那么今天，我们来通过以下动画来感受一下工程师们那不亚于艺术家的机械设计的美感吧。 

1、飞机的星形发动机 

 

 

燃气发动机 

 

喷气发动机 

 

2、椭圆规 

 

3、缝纫机 

 

4、马耳他十字机芯——用于控制时钟的秒针运动 

 

5、汽车变档机制 

 

6、汽车等速万向节，我终于明白为啥前轮驱动的骑车的轮子还能转 

 

7、舰炮弹药装填系统，原来推进药跟战斗部是分着的啊 

8、转子发动机——内燃机的一种，把热能转为旋转运动而非活塞运动，如马自达RX8 

 

 

9 直列式发动机——它的汽缸肩并肩地排成一排，L4发动机，一般的车都用 

 

10、V 型发动机 ——汽缸排列在成一定角度的两个平面上，V6发动机 

 

11、水平对置式发动机 ——汽缸排列在发动机相对的两个平面上，保时捷911用的是这种的6缸 

 

手枪 

 

 

左轮 

奎西发动机 

 

斯特林发动机 

 

其他的小发动机 

 

其他 

 

 

 

 

 

 

 

 

 

Orignal From: 手枪、多种发动机的机械原理图解

发表于 更新于 分类于 阅读次数： Valine：

 

英文原文：10 Myths About Introverts

作者：Carl King

我非常幸运的发现了这本《内向者优势——如何在外向的世界中获得成功》的好书，我感觉就好像是有人专门为我们这个罕见的小群体写了一部百科全书一样，它不仅对我的很多怪癖做了解释，还帮助我从一个崭新且积极的角度重新定义了我的整个人生。

 

毫无疑问，几乎所有认识我的人都会说，“啊哈，你不会到现在才发现你是个性格内向者吧？”，其实这并不是那么简单，问题在于将一些人贴上内向者的标签是一种非常浅显且充满各种常见误解的行为，事实要比这复杂的多（在Carl King讲过之后，就更是如此了）

Laney的书中有个章节对人的大脑进行了分析，并解释了神经元是如何在内向者和外向者的神经系统中跟随不同的控制通路进行传递。如果这本书基于的科学理论是正确的，那就证明了内向者是一群对多巴胺过度敏感的群体，太多的外部刺激过量的消耗了它们。相反的，外向者没有足够的多巴胺，他们需要依靠大脑的肾上腺去创造它们，外向者通常有更短的神经通路，他们的大脑血流量也相对更少，外向者神经系统中的信息大部分都是通过位于前额叶的布罗卡氏区（Broca’s area）传递的，而这里正是我们的大部分思考发生的地方。

不幸的是，根据这本书，只有大约25%的人是内向的，而像我这样极端的就更是少上加少了，这导致了许多的误解，因为社会对我们这类人缺乏足够的了解（我很高兴我能够这样说）

所以下面我列出了一些对内向者的常见的误解（这是我自己的清单，我对其中一些深信不疑）：

误解1： 内向者不喜欢说话

并不是这样，内向者不说话只是因为他们觉得没什么好说，他们讨厌闲谈扯淡，如果你让一个内向者讲他感兴趣的事情，他可能连着3天3夜都讲不完。

误解2： 内向者都很害羞

内向者没什么好害羞的，他们也不是害怕陌生人，他们只是需要一个理由去交际，他们不会为了交际而交际，如果你想和一个内向者交流，那就直接聊吧，不用担心礼貌问题。

误解3：内向者都很无礼

内向者通常觉得遵从社交礼仪，拐弯抹角的说话没有一点必要，他们希望每个人都是真实且真诚的，但不幸的是，大多数情况下事情并不是这样，这让内向者感到很大的压力，他们很难融入其中，并为此感到沮丧。

误解4： 内向者不合群

恰好相反，内向者会非常认真的对待他们为数不多的朋友，他们最亲密的朋友或许用一只手就可以统计过来，但如果你有幸被一个性格内向者当做朋友，那你就有了一个终生的盟友，一旦你作为一个人类存在赢得了他们的尊敬，你就入选了。

误解5：内向者不喜欢去公共场合

胡扯，内向者只是尽可能的避免去公共场所，他们同样也会尽量避免卷入复杂的公共活动，因为他们可以在极短的时间内获取需要的数据和经验，所以，他们喜欢在一个地方待很久去“得到某样东西”，他们总是准备着回家，调整（Recharging），然后处理一切，实际上，调整绝对是内向者的关键所在。

误解6：内向者总是想要独处

内向者只是喜欢自我思考，他们会想很多，他们会白日做梦，他们喜欢解决问题，攻克难题，但是如果他们找不到什么人来分享他们的发现，他们也能忍受难以想象的孤独。他们希望在同一时间只和一个人保持亲密的感情关系。

误解7：内向者都很古怪

内向者通常都是个人主义者，他们不喜欢随大流，他们喜欢通过特立独行的生活方式来体现自己的价值，他们总是从自我出发，正因如此，他们也常常挑战常规，他们的大部分决定都不会以当前的流行趋势做为参考。

误解8：内向者都是冷漠的书呆子

内向者通常更关注内心世界，他们将更多的精力放到自身的想法和感情上，但这并不代表他们对他们身边的事情漠不关心，只是他们更喜欢通过内心世界来达成自我满足。

误解9：内向者不知道如何放松和享乐

内向者通常喜欢在家或自然中放松自己，他们不会去那些嘈杂的公共场所，内向者也不会寻求肾上腺素的刺激，如果有太多的空谈和噪音，他们会敬而远之。他们的大脑对于一种叫做多巴胺的神经递质太过敏感，内向者和外向者拥有完全不同的神经控制通路，关于这一点，你可以深入了解下。

误解10：内向者可以通过“自我修复”变得外向

想象一个没有内向者的世界，那个世界也就没有什么科学家，音乐家，艺术家，诗人，制片人，医生，数学家，作家和哲学家了，之所以这么说，是因为外向者还是可以通过学习掌握很多种和内向者进行交流的方式（没错，我故意颠倒了这两个词，读着很别扭？我只是为了让你们看看我们这个社会有多变态），内向者压根不需要“自我修复”，他们应该因为他们这种天生的性格和为人类做出的贡献而得到应有的尊敬，并且事实上，一项调查（Silverman，1986）显示内向的程度和IQ成正比。

“你没法避开我们，尝试改变我们只会让你感到失败”，这是我编的，我是一名剧作家。

内向者如果为了去适应外向者支配的世界而对自己进行否定，结果将会是灾难性的，内向者终将会仇恨自己以及其他所有人。如果你认为你是个内向者，我推荐你研究下这个题目并试着找其他的性格内向者交换下意见，问题并不完全是内向者应该尝试并“变得正常”，外向者也需要认识和尊敬我们，并且我们也需要学会尊敬我们自己。

发表于 更新于 分类于 阅读次数： Valine：

 

 

TimThumb是一个简洁高效的创建图片缩略图的程序。它功能非常强大，并且制定性很强。通过对多个参数的控制，你可以灵活地设置缩略图片的输出样式。

 

然而，有时候具体应用时，会产生一些性能问题。由于它的调用方式

 

<IMG alt=”" src=”/scripts/timthumb.php?src=/images/whatever.jpg&h=150&w=150&zc=1″>

 

服务器可能不会自动对图片进行压缩，也不会自动添加图片的客户端缓存过期时间。下面我们来看一下如何解决这些问题。

 

开启cache

TimThumb是有cache功能的，如果你的图片没有cached，请查看timthumb.php文件第45行左右

 

check_cache….

移除前面的#或//符号，这将使服务器响应时间加快5倍（100ms降低到20ms）。

 

修改cache目录

 

最好将cache目录设为网站上传目录（upload目录）（有人如此建议）。第35行：

 

$cache_dir = ‘./cache’;

 

计算timthumb.php文件所在目录深度，.将cache_dir设为../… /uploads/

 

设置最大压缩比

PNG图片的最后一个参数不是质量级别而是压缩级别。我们可以单独修改这个参数达到最大压缩比。

 

找到timthumb.php文件第174行左右

 

$quality = floor($quality * 0.09);

在下面添加：

 

$quality = 9;

加快图片的载入速度

 

你可以把以下规则添加进你的.htaccess文件中，可加速图片载入速度：

 

RewriteEngine on

 

RewriteRule .* – [E=HTTP_IF_MODIFIED_SINCE:%{HTTP:If-Modified-Since}]

 

RewriteRule .* – [E=HTTP_IF_NONE_MATCH:%{HTTP:If-None-Match}]

 

设置客户端缓存

将第317行左右的最大有效期设为：

 

header(“Cache-Control: max-age=315360000,public”);

 

下两行左右位置，设为：

 

header(“Expires: ” . gmdate(“D, d M Y H:i:s”, time() + 315360000) . “GMT”);

 

设置静态地址

将图片的动态地址改为静态地址也会加快服务器的响应速度。

 

参考：

 

http://www.speedingupwebsite.com/2010/02/11/hacking-timthumb-php-all-the-best-practices/

 

关于timthumb.php更多用法：

 

http://code.google.com/p/timthumb/

发表于 更新于 分类于 阅读次数： Valine：

晒图是个简单易用的照片处理工具，是你在网上发布照片的好帮手

基本功能有三个:

 

高级功能包括:

  • 圆角大小调节
  • 三种可选EXIF外框
  • 水印透明度、颜色、字体调节
  • 照片批量处理
  • 照片输出质量控制
  • 照片输出大小控制
  • 照片输出质量预览、输出大小预告
  • 三种主题
  • 中英文菜单切换

 

晒图无需安装，解压即可运行，另外还提供了非常方便的自动升级支持

主界面截图：

 

详细介绍请查看项目地址：http://code.google.com/p/shaitu/

发表于 更新于 分类于 阅读次数： Valine：

GA

Google Analytics v5 新版首次增加了新功能：页面速度报告。了解了不同人群访问网页的载入速度才能有针对性的进行优化，进入新版后，在左侧的Content里的Site Speed即可看到统计，包括：

  • 哪个页面读取的最慢
  • 不同地区的人们访问速度有何区别
  • 在不同浏览器里的读取速度如何
  • 哪个来源的读取速度最快

要得到数据报告需要修改你的GA分析代码。 具体修改方法见这里，目前只有英文的介绍。修改之后类似这样：

1
2
3
4
5
6
7
8
9
10
11
12
<script type="text/javascript">
 var _gaq = _gaq || [];
 _gaq.push(['_setAccount', 'UA-XXXXX-X']);
 _gaq.push(['_trackPageview']);
 **_gaq.push(['_trackPageLoadTime']);**

 (function() {
   var ga = document.createElement('script'); ga.type = 'text/javascript'; ga.async = true;
   ga.src = ('https:' == document.location.protocol ? 'https://ssl' : 'http://www') + '.google-analytics.com/ga.js';
   var s = document.getElementsByTagName('script')[0]; s.parentNode.insertBefore(ga, s);
 })();
</script>

修改之前的代码可能是这样的：

1
2
3
4
5
6
7
8
9
10
11
12
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>

<script type="text/javascript">
try{
 var pageTracker = _gat._getTracker("UA-xxxxxx-x");
 pageTracker._trackPageview();
 **pageTracker._trackPageLoadTime();**
} catch(err) {}
</script>

发表于 更新于 分类于 阅读次数： Valine：

The story

Beijing, China-based startup, DianDian, has recently raised $10 million from big names like Sequoia and Ceyuan. With more than $1 million capital it seized from Kai-Fu Lee’s Innovation Works in Feburay, DianDian has raised a total of $11 million or more in just several months.

You might wonder what kind of service DianDian provides. Actually it is a Tumblr clone in Chinese. It is a high level of imitation and the biggest difference you can tell is that the website is in Chinese.

DianDian vs Tumblr

Check the screenshots below.

login

Comparing Login Buttons

editing

Comparing “Editing a post” UI

dashboard

Comparing Dashboard UI

The Discussions

After the news came out on April 7, people began discussing it on Zhihu, a clone of Quora which also got funded by Kai-Fu Lee’s Innovation Works. The users are quickly divided into 2 groups.

One group with Innovation Works’s co-founder, lawyer and senior managers are supporting Innovation Works’s decision, while most entrepreneurs and programmers are against that.

Jixin Huang, Senior Manager of Innovation Works responds (digest):

It’s coarse to call Diandian “a 100%-copycat”

Innovation Works invests in DianDian because they create something more than just cloning.

Hua Wang, Co-founder of Innovation Works responds (digest):

The discussion has no meaning because we are making our decisions based on the forecast of Chinese users, market and the industries.

Benjamin Qiu, Lawyer of Innovation Works responds (digest):

It’s hard to agree, but the conclusion is that UI is not protected by law, just because it is not artistic enough, not original enough.

The UI presented here means buttons, banner’s position, combination of color and etc. And all the elements have been used somewhere else before.

… If the percentage of the similarity is up to 90% it won’t violate any law in China, even in U.S.

While the opposite opinion is simple but powerful: the user called “Hi-iD” answers:

You can’t do that, unless you are a thief, a bandit or a mafia!

Whose Cheese Got Moved?

Although obviously Kai-Fu Lee is not the only one who made this happen. People began making jokes of his name on Twitter. One joke says Kai-Fu is really the short for Kai-Shi-Fu-Zhi Lee, in which ‘Kai-Shi’ means ‘Start’ and ‘Fu-Zhi’ means ‘Copy’.

And several hours ago, someone built a website called Copy Works using a theme ripped off from Innovation Works’s homepage. People began to register with user names like Kai-Shi-Fu-Zhi, Kai-Shi-Lee in Weibo, a Twitter-like service in China.

copy works

Screenshot of copy-works, a theme ripped off from Innovation Works’s homepage

Former VP of Google, Kai-Fu Lee is an icon of success in China. He had written six open letters to students in China and one open letter to their parents, and thus acknowledged as the mentor for students. He also runs a web site named Kai-Fu & Students’ under his own name http://kaifulee.com. His first open letter in year 2000 to students titled About honesty and integrity. You can imagine how you would react when someone who told you to be honest did something against common morality.

Till now, there’s no official statements or apologies from DianDian or from Innovation Works.

—-
Many thanks for @kimseong on proofreading this tip.

Source:http://jyorr.com/post/4622300101/former-google-vp-kai-fu-lee-got-a-nickname-start-copy

发表于 更新于 分类于 阅读次数： Valine：

2011年4月10日，下午2点40分，在网吧里，听着《眼泪的错觉》。突然间的感觉，记忆回到从前！回忆可停留，但时光已不在。

为什么剩我一人孤单守候，能不能再陪我说句话。这边的环境很安静，好久没有出来了，这两天不再加班，远离了办公室，来到了稍远的地方，以为就在城市边缘，没有烦扰。外面的空气很温柔，阳光也很安静，还有桃花与其它不知道名字的花儿。还有一个很大的半个公园，如果有时间在这儿好好享受那是多么的惬意。

与朋友只是偶尔回忆下过去了，好像现在的回忆比过去更加的愁绪。小时候想着快点长大，长大的时候想再重复一次。你我都知道，最美的风景永远在远方，生活在别处！

网吧的网速很快，即使有其他人下载看电影也不要闹情绪了，除了空气不是太好外，其它的还好。等会，我就要回去了，就好像一个时代要结束了。

这个周末过的不错，没有加班！

发表于 更新于 分类于 阅读次数： Valine：

微软的IE Developer Toolbar，这是一个免费的专门为Web开发人员制作的IE插件，IE插件IEDevToolBar可以帮助我们分析网站的布局结构，有助于我们学习和分析页面的CSS，其主要功能有：

1.以树结构查看CodeDom，并查看每个Element属性，可以使用鼠标点击选中Element，这个在我们制作和调试网页时很有用；

2.生成图片报表，就是将页面上说有出现的图片生成一份详细的报表，这样就省的我们自己去找图片路径和量图片大小等等；

3.高亮显示表格，表格单元，Div等的边框，这个在我们调整布局时也是很有用；

4.页面尺子，可以然你任意在页面上度量长度，这个是大大的提高了我们的工作效率，不用为了量个长度而抓图再用画图工具量。

安装之后，在IE顶部菜单的“查看” － “工具栏” 里面钩选“Developer Toolbar”项即可。这下在IE下做 Web开发就方便多了！

0%